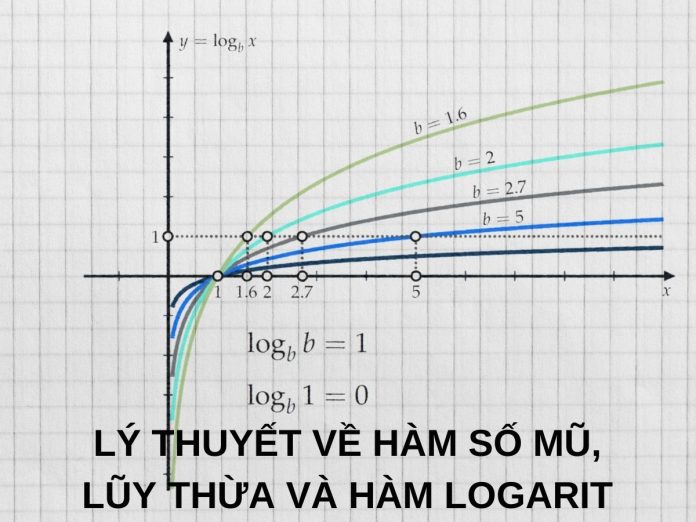
Hàm số mũ, hàm số logarit là những khái niệm quen thuộc với tất cả các bạn học sinh THPT. Đây được xem là phần quan trọng và chiếm nhiều câu hỏi trong cấu trúc đề thi Toán tốt nghiệp THPT các năm gần đây.
Các câu hỏi về hàm số mũ và hàm số Logarit trải dài trên 3 4 dạng câu hỏi: nhận biết, thông hiểu, vận dụng và vận dụng cao trong đề thi. Chính vì vậy, các bạn học sinh cần phải chú trọng trong việc ôn luyện và làm bài tập nhuần nhuyễn. Hãy cùng luyenthidgnl cùng tìm hiểu về lý thuyết về hàm số mũ, hàm số Logarit nhé!
Mục lục
Lý thuyết về hàm số mũ, hàm số logarit
1. Hàm số mũ
1.1 Định nghĩa hàm số mũ
Cho một số thực dương a (điều kiện a khác 1)
- Ta có hàm số:
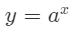
Đây là hàm số mũ với cơ số a
Ví dụ: y = x^3 là hàm số mũ cơ số 3
1.2 Các tính đạo hàm của hàm số mũ
Trong chương trình học THTP, ta không đi quá sâu vào việc phải chứng mình công thức nên ta thừa nhận công thức sau:
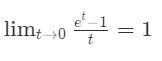
- Định lý 1: Hàm số y = e^x có đạo hàm tại mọi x và:

Ví dụ: (e^2x)’ = (2x)’e^2x = 2e^2x
- Định lý 2: Hàm số y = a^x có đạo hàm tại mọi x và:

1.3 Khảo sát đồ thị của hàm số mũ
Dưới đây là khảo sát hàm mũ y = a^x với điều kiện a > 1 và hàm số mũ y = a^x với điều kiện .

2. Lý thuyết về hàm số Logarit
2.1 Khái niệm về hàm số Logarit
Cho một số thực dương a≠1
Hàm số có dạng y= logax được gọi là hàm số Logarit cơ số a
2.2 Đạo hàm của hàm số Logarit
y= logax (với điều kiện a>0 và a≠1) có đạo hàm với mọi x > 0 và:
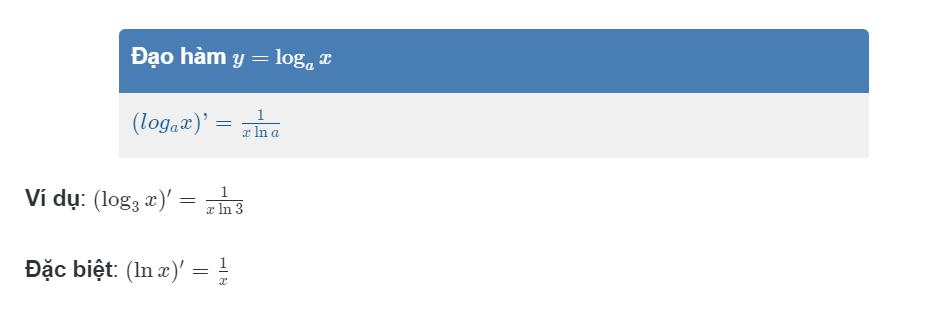
2.3 Khảo sát hàm số Logarit
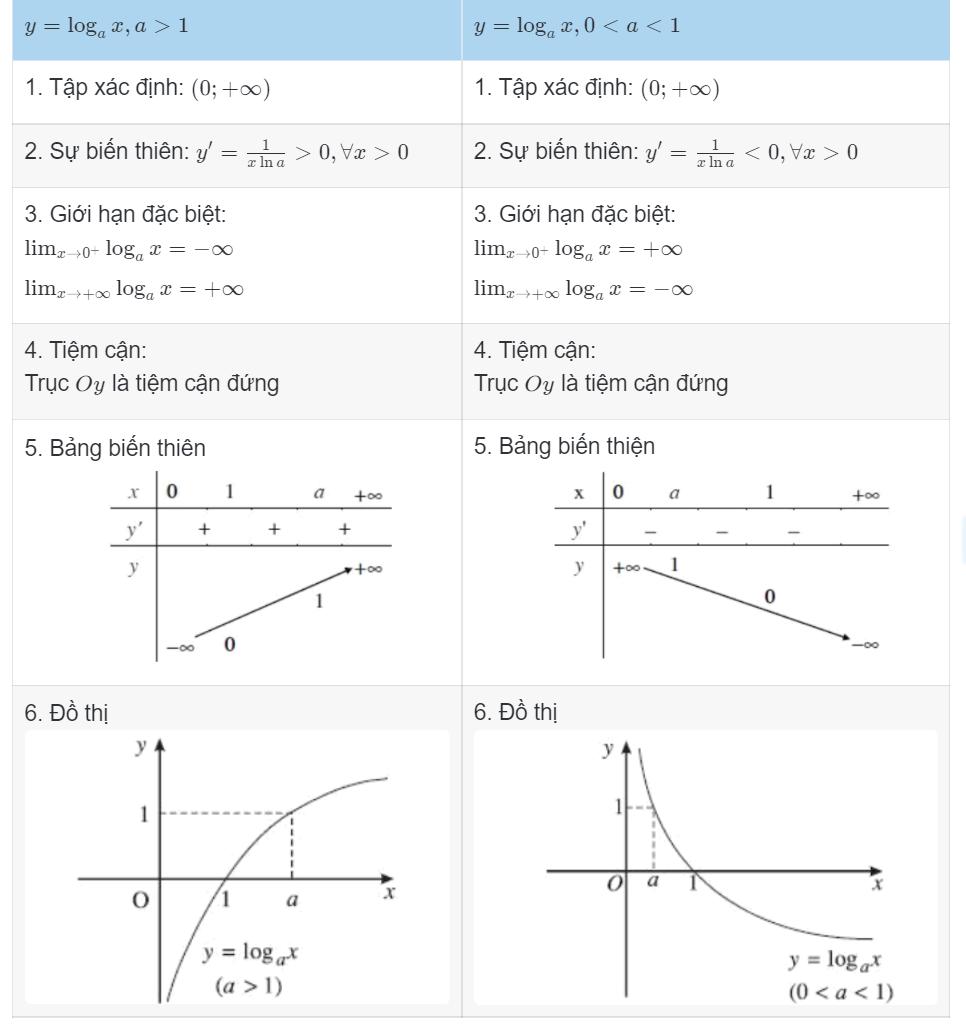
3. Bảng tổng hợp đạo hàm của các hàm số mũ, lũy thừa và hàm số logarit

Trên đây là hệ thống các kiến thức cơ bản nhất về hàm số mũ và hàm số Logarit dành cho các bạn đang trong giai đoạn ôn thi tốt nghiệp THPT Quốc Gia môn Toán. Hy vọng thông qua bài viết sẽ giúp các bạn đạt kết quả tốt nhất trong kỳ thi sắp tới!
Các bạn có thể tham khảo các bài viết liên quan:
Bộ đề thi tốt nghiệp THPT quốc gia mới nhất – môn toán
Khảo sát biến thiên hàm số và vẽ đồ thị















