Trong kỳ thi tốt nghiệp THPT quốc gia môn toán, các câu hỏi về khối đa diện cũng thường xuyên xuất lượng và chiếm số lượng không nhỏ (thường từ 3 đến 4 câu). Chính vì vậy các kiến thức về khối đa diện các bạn học sinh cũng cần thực sự lưu ý trong quá trình ôn thi Toán tốt nghiệp THPT. Chính vì vậy, luyenthidgnl xin được chia sẻ các kiến thức cần nắm được về khối đa diện cũng như các công thức để áp dụng trong quá trình làm bài.
Các bạn có thể tham khảo thêm: Cấu trúc đề thi môn toán tốt nghiệp THPT 2022
Mục lục
Khối đa diện là gì?
1. Khái niệm về hình đa diện
Hình đa diện ( hay có cách gọi tắt là đa diện) là hình được tạo thành bởi một số hữu hạn các đa giác thỏa mãn các tính chất sau:
b) Mỗi cạnh của đa giác bất kỳ phải là cạnh chung của chỉ 2 đa giác
Mỗi đa giác như vậy được gọi là một mặt của hình đa diện . Các đỉnh và cạnh của các đa giác ấy lần lượt được gọi là các đỉnh, cạnh của hình đa diện.
2. Khái niệm về khối đa diện
Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả bao gồm bề mặt hình đa diện đó
Tất cả những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện.
Các điểm thuộc khối đa diện nhưng không nằm trên hình đa diện ứng của khối đa diện ấy được gọi là điểm trong của khối đa diện. Tập hợp những điểm trong là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
Các khối đa diện được xác định bởi cácd hình đa diện ứng với nó. Ta cũng gọi đỉnh, cạnh, mặt, điểm trong, điểm ngoài… của một khối đa diện theo thứ tự là đỉnh, cạnh, mặt, điểm trong, điểm ngoài… của hình đa diện tương ứng.
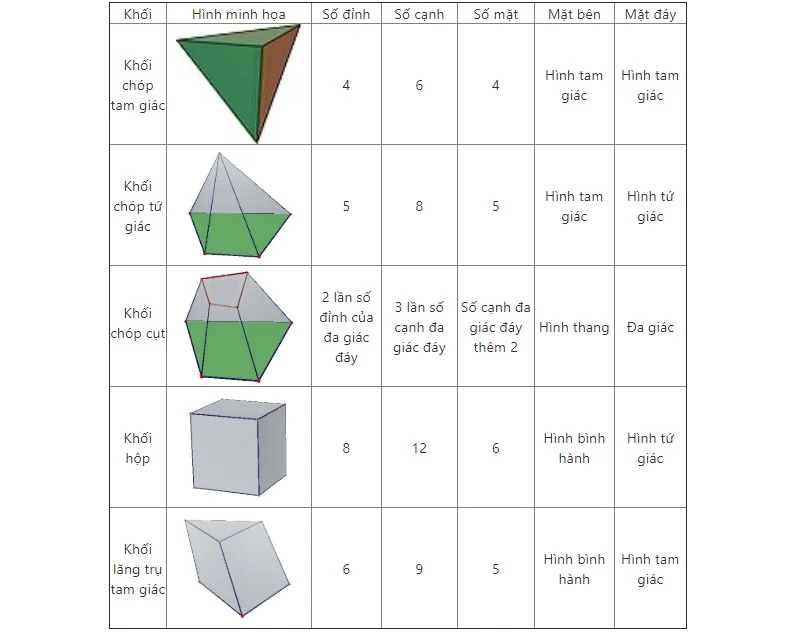
Một số ví dụ về khối đa diện:
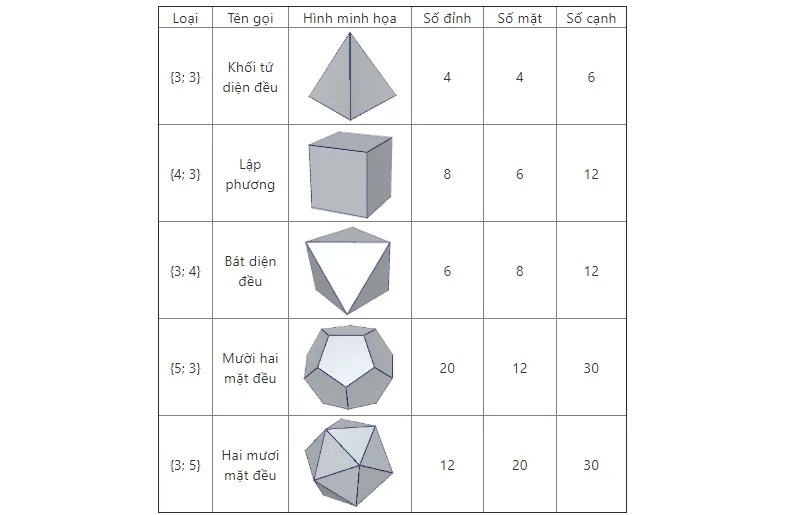
Các loại khối đa diện thường gặp
Phân chia khối đa diện
Cho một khối đa diện (H) là tập hợp của hai khối đa diện (H1) và (H2) thỏa mãn điều kiện:
(H1) và (H2) không có bất cứ điểm chung trong nào thì ta nói (H) có thể phân chia được thành 2 khối (H1) và (H2). Bên cạnh đó, ta cũng có thể nói ghép hai khối (H1) và (H2) ta được khối đa diện H
Ví dụ: Cắt hình lăng trụ ABC.A’B’C’ bởi mặt phẳng (A’BC) ta có hai khối đa diện mới là A’ABC và A’BCC’B’.
Một số tính chất đặc biệt về khối đa diện
Tính chất 1: cho một khối tứ diện đều:
+ Trọng tâm của các mặt của khối tứ diện là đỉnh của một khối tứ diện đều khác.
+ Trung điểm của các cạnh của khối tứ diện đều là các đỉnh của một khối bát diện đều (khối đa diện có 8 mặt đều nhau).
Tính chất 2: Trong một khối lập phương, tâm các mặt của nó sẽ tạo thành 1 khối bát diện đều.
Tính chất 3: Dối với một khối bát diện đều, tâm các mặt của nó sẽ lần lượt là đỉnh của một khối lập phương.
Tính chất 4: Hai đỉnh của một khối bát diện đều được gọi là hai đỉnh đối diện khi và chỉ khi chúng không thuộc cùng một cạnh của khối bát diện đó. Đoạn thẳng được tạo ra bởi hai đỉnh đối diện được gọi là đường chéo của khối bát diện đều. Khi đó ta có:
+ Ba đường chéo cắt nhau giao nhau tại trung điểm mỗi đường.
+ Ba đường chéo vuông góc với nhau theo từng cặp
+ Ba đường chéo có chiều dài bằng nhau.
Tính chất 5: một khối đa diện phải có ít nhất 4 mặt.
Tính chất 6: Hình đa diện có ít nhất 6 cạnh.
Tính chất 7: Không tồn tại khối đa diện có 7 cạnh.
Các công thức tính thể tính khối đa diện
- Công thức tính thể tích hình chóp
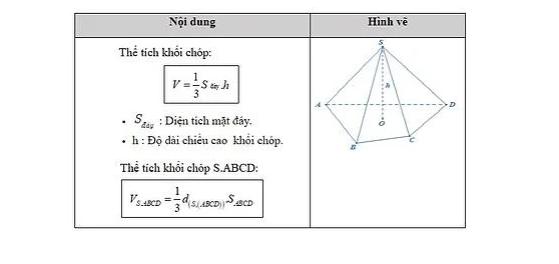
2. Công thức tính thể tích hình hộp chữ nhật

3. Công thức tính thể tích khối lăng trụ
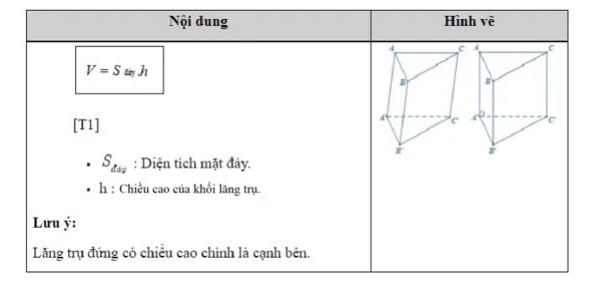
4. Công thức tính tỉ số thể tích
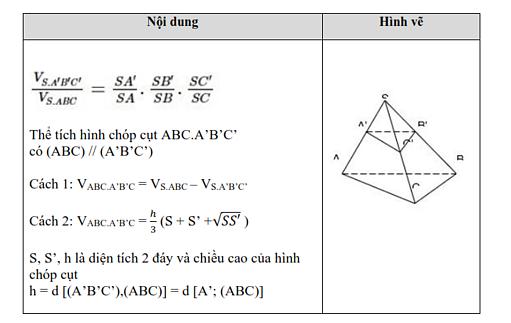
5. Công thức nâng cao

Trên đây là kiến thức cần biết về khối đa diện mà các bạn cần nắm được để chuẩn bị cho kỳ thi tốt nghiệp THPT môn Toán. Chúc các bạn đạt được kết quả cao trong kỳ thi sắp tới!
Một số bài viết các bạn có thể tham khảo thêm:
Logarit là gì? công thứ, đạo hàm và các dạng bài tập
Số phức – Tổng hợp kiến thức cơ bản và các công thức số phức